Generalized Lotka–Volterra equation

The generalized Lotka–Volterra equations are a set of equations which are more general than either the competitive or predator-prey examples of Lotka–Volterra types.[1][2] They can be used to model direct competition and trophic relationships between an arbitrary number of species. Their dynamics can be analysed analytically to some extent. This makes them useful as a theoretical tool for modeling food webs. However, they lack features of other ecological models such as predator preference and nonlinear functional responses, and they cannot be used to model mutualism without allowing indefinite population growth.

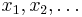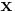The Generalised Lotka-Volterra equations model the dynamics of the populations x_1, x_2, \dots of n biological species. Together, these populations can be considered as a vector \mathbf{x}. They are a set of ordinary differential equations given by

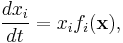
\frac{dx_i}{dt} = x_i f_i(\mathbf{x}),

where the vector 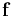\mathbf{f} is given by

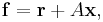
\mathbf{f} = \mathbf{r} %2B A\mathbf{x},

where 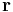\mathbf{r} is a vector and A is a matrix known as the community matrix.

Contents

Meaning of parameters

The generalised Lotka-Volterra equations can represent competition and predation, depending on the values of the parameters, as described below. They are less suitable for describing mutualism.

The values of 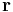\mathbf{r} are the intrinsic birth or death rates of the species. A positive value for 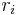r_i means that species i is able to reproduce in the absence of any other species (for instance, because it is a plant), whereas a negative value means that its population will decline unless the appropriate other species are present (e.g. a herbivore that cannot survive without plants to eat, or a predator that cannot persist without its prey).

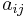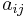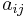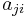The values of the matrix A represent the relationships between the species. The value of a_{ij} represents the effect that species j has upon species i. The effect is proportional to the populations of both species, as well as to the value of a_{ij}. Thus, if both a_{ij} and a_{ji} are negative then the two species are said to be in direct competition with one another, since they each have a direct negative effect on the other's population. If 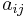a_{ij} is positive but 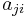a_{ji} is negative then species j is considered to be a predator (or parasite) on species j, since i's population grows at j's expense.

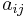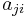Positive values for both a_{ij} and a_{ji} would be considered mutualism. However, this is not often used in practice, because it can make it possible for both species' populations to grow indefinitely.

Indirect negative and positive effects are also possible. For example, if two predators eat the same prey then they compete indirectly, even though they might not have a direct competition term in the community matrix.

The diagonal terms 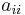a_{ii} are usually taken to be negative (i.e. species i's population has a negative effect on itself). This self-limitation prevents populations from growing indefinitely.

Dynamics and solutions

The Generalised Lotka-Volterra equations are capable of a wide variety of dynamics, including limit cycles and chaos as well as point attractors (see Hofbauer and Sigmund). As with any set of ODEs, fixed points can be found by setting 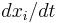dx_i/dt to 0 for all i, which gives

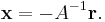
\mathbf{x} = -A^{-1}\mathbf{r}.

This may or may not have positive values for all the x_i; if it does not then there is no stable attractor for which the populations of all species are positive. If there is a fixed point with all positive populations it may or may not be stable; if it is unstable then there may or may not be a periodic or chaotic attractor for which all the populations remain positive. In either case there can also be attractors for which some of the populations are zero and others are positive. 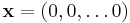\mathbf{x}=(0,0,\dots 0) is always a fixed point, corresponding to the absence of all species.

See also

References

  1. ^ Metz, J. A. J.; Geritz SAH, Mesz´ena G, Jacobs FJA, van Heerwaarden JS (1996). "Adaptive dynamics, a geometrical study of the consequences of nearly faithful reproduction.". In van Strien SJ, Verduyn Lunel SM (book). Stochastic and Spatial Structures of Dynamical Systems, Proceedings of the Royal Dutch Academy of Science (KNAW Verhandelingen) (IIASA Working Paper WP-95-099. ed.). North Holland, Amsterdam: Elsevier Science Pub Co.. p. 183–231. ISBN 0444858091. http://www.iiasa.ac.at/Publications/Documents/WP-95-099.pdf. Retrieved 2009-09-20. 
  2. ^ Hofbauer, Josef; Karl Sigmund (1998) (book). Evolutionary Games and Population Dynamics.